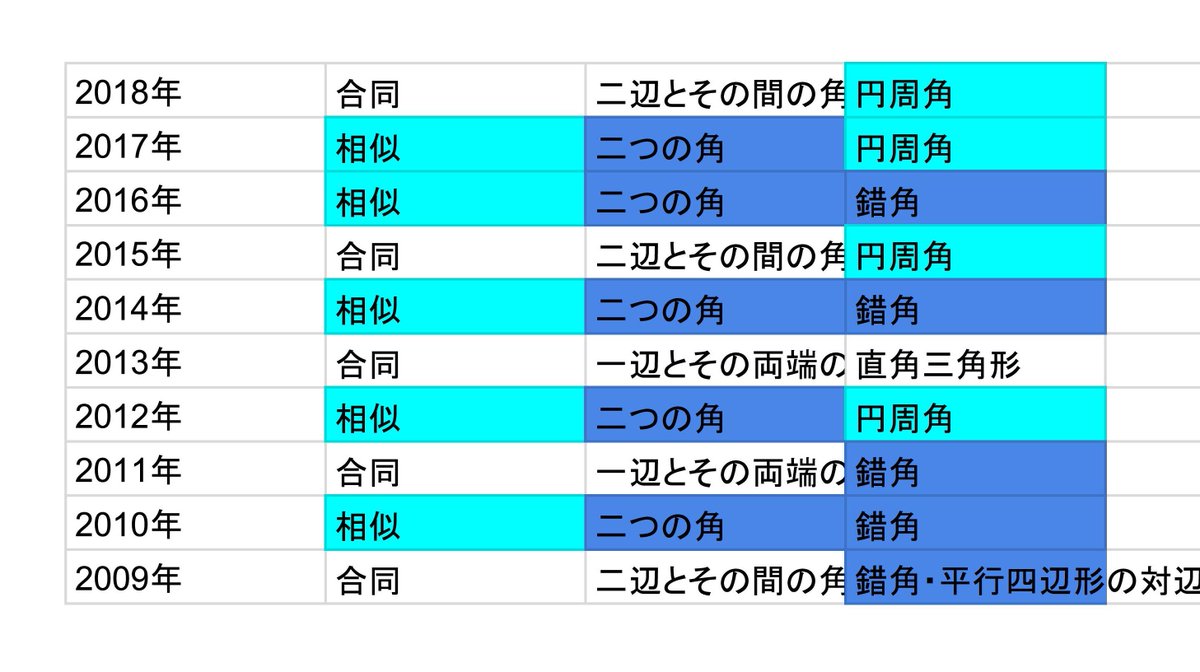
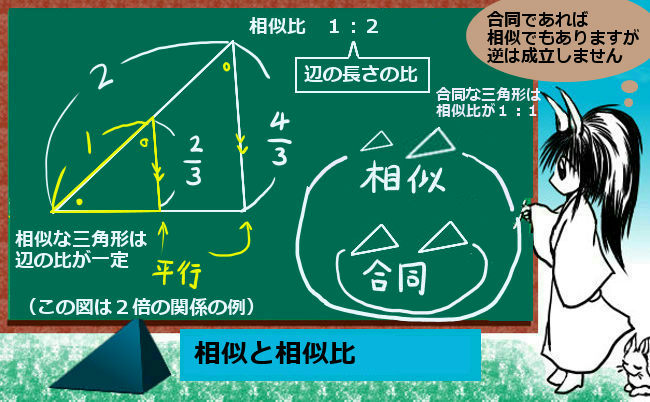
27/1/ 現役講師がわかりやすく解説! 今回学んでいくのは、相同器官、相似器官、痕跡器官だ。 中学や高校の授業では、生物の進化などを学習するときにみられる用語だが、良く似た言葉がいくつか出てくるため混同してしまうやつも少なくないな。 それぞれの言葉の意味をしっかり押さえ、違いが分かるようにしよう。 大学で生物学を学び、現在は講師としても活動一部の表現が不明瞭である.(1) 例えば,合同や相似の定義と性質の違いが,意 図的だと予想するが,数学的には不明瞭である.(直観的) ユークリッド的定義と証 明されるべき性質とが区別されていないが,大学で数学をほとんど学ばなかった小相似比 k が m:n で与えられている相似形 F ,F′ においては,対応する角が等しく,対応する部分の長さの比は m:n ,面積の比は m 2 :n 2 ,体積の比は m 3 :n 3 となる。互いに合同な図形は,相似比が1の相似形と考えられる。
合同とは 相似とは
合同 相似 違い
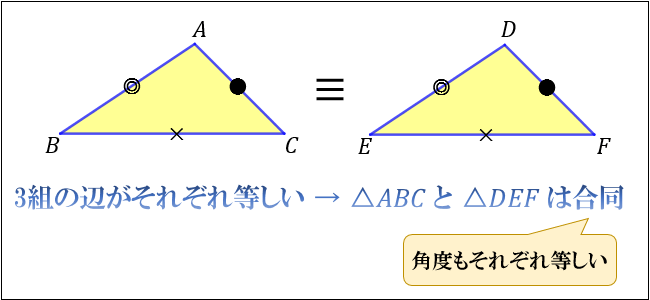
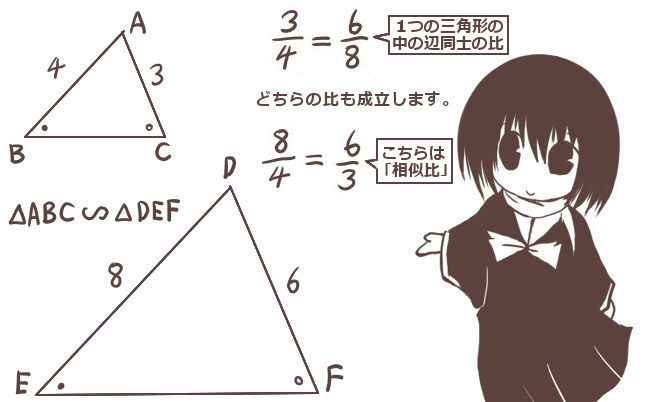
合同 相似 違い- こんにちはtanukiです。 今回は相似についての記事ですが学習ポイントとかではなく教え方の話です 。 たまに長年算数を教えている先生でも 「相似とは形が同じで大きさがちがう図形の関係のこと」 と説明される方に出会います。 「形も大きさも同じ」合同と比較しての説明なのでしょう。 合同条件と相似条件には2つあるよ。 合同条件3「 2つの辺とその間の角がそれぞれ等しい」 最後の合同条件は、 2つの辺との間の角がそれぞれ等しい ってヤツ。 等しい辺たちが等しい1つの角を挟んでいれば、2つの三角形は合同って言えるんだ。



相似と合同の違いは Yahoo 知恵袋
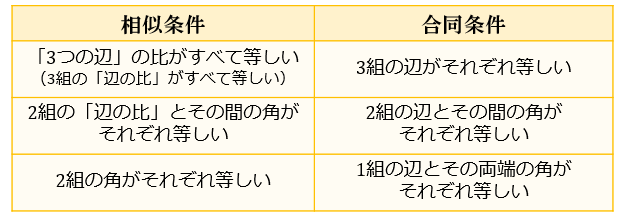
証明問題 (合同・相似)の解き方 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用の 主な違い クラス図とオブジェクト図の違いは、 クラス図はクラスとそれらの間の関係を表し、オブジェクト図は特定の瞬間のオブジェクトとそれらの間の関係を表します umlは統一モデリング言語の略です オブジェクト指向の概念をモデル化してソフトウェアソリューションを開発するの24/6/12 合同・相似条件の書き方 三角形の合同条件と相似条件の書き方は次の通りです。 三角形の合同条件 3組の辺 がそれぞれ等しい。 2組の辺とその間の角 がそれぞれ等しい。 1組の辺とその両端の角 がそれぞれ等しい。 三角形の相似条件 3組の辺の比 が
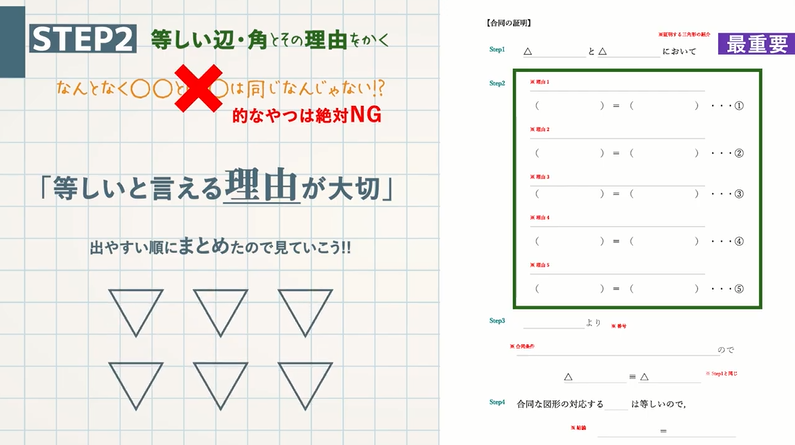
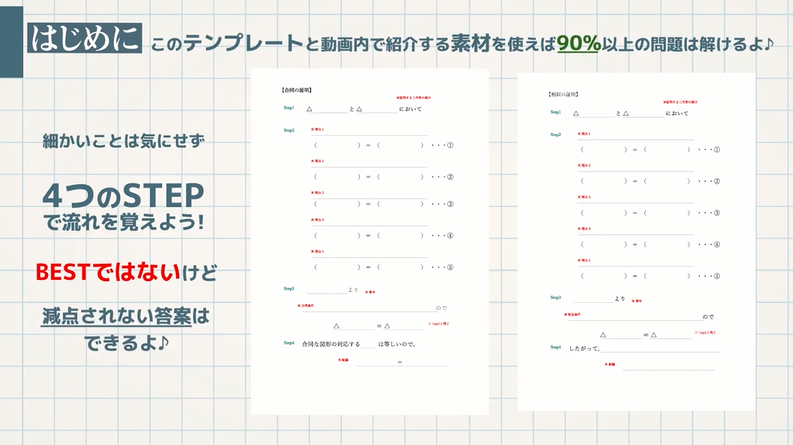
ー 45 ー 1 次 方 へ程 式 平 方 根 2 次 方 程 式 関 数 へと グ ラ フ 平面図形 合 同 と 相 似 三 平 方 の 定 理 19 NHK高校講座〈ベーシック数学〉証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch laterイプシロン 09 Vol 51, 2935 集合の考えを生かした図形指導の一考察 愛知教育大学 影 山 和 也 1 はじめに van Hieleの幾何的思考水準論は広く初等中等教育さらにそれ以上の範囲をカバーするが,
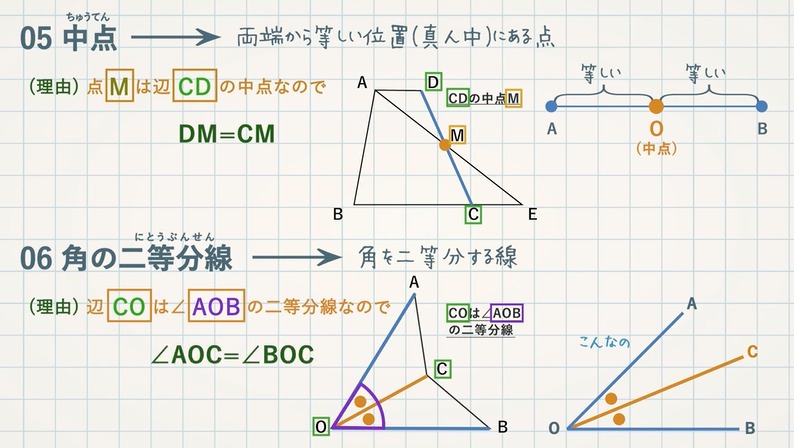
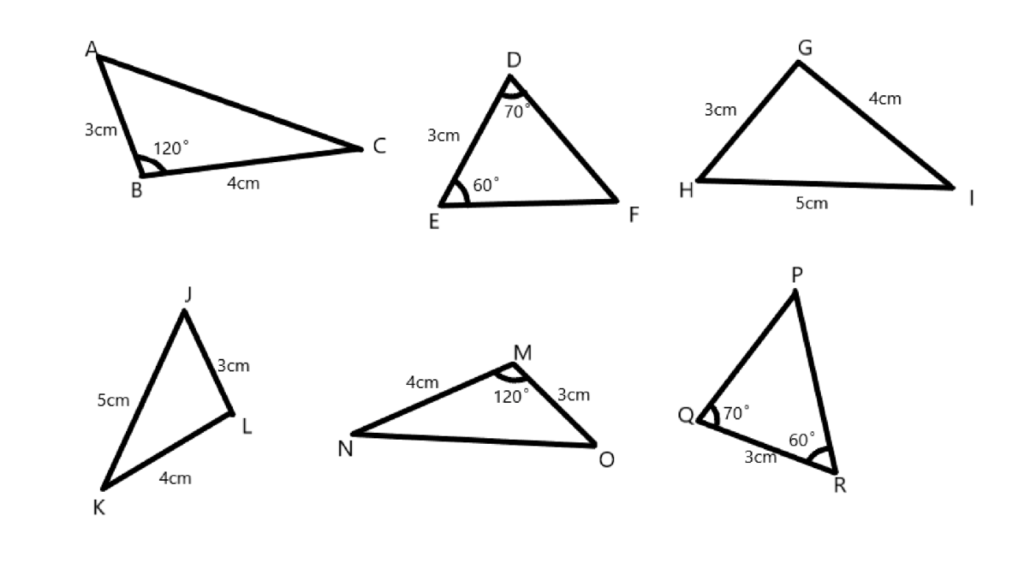
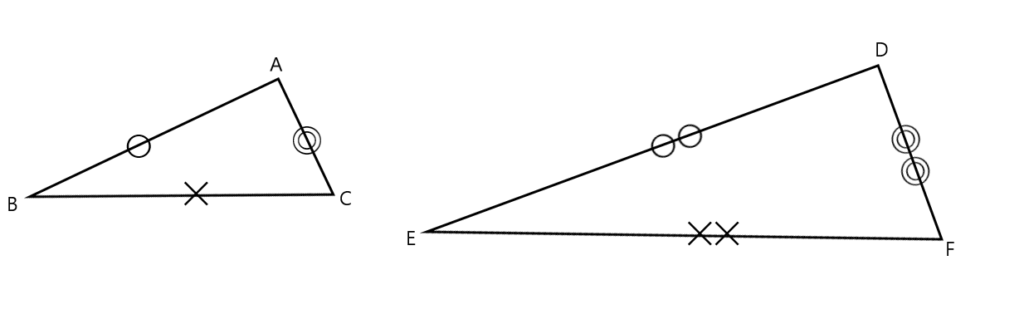
この3つの中から相似な図形を見つけるときに 情報が少ない図形は、相似条件に当てはめることができません。 なので、情報が多く揃っている ABCと ABDが相似になるだろうな、と予想して この2つの三角形が、相似条件に当てはまるかを確かめていきます2つの条件の違い(解答例) 合同条件は,対応する辺の長さがそれぞれ等しい が,相似条件では,対応する辺の比はすべて等し い。 合同条件の「1辺とその両端の角がそれぞれ等し い。」に対して,相似条件では,「2組の角がそれ ぞれ等しい。26/4/21 相似(そうじ)とは。意味や解説、類語。名(スル)1 形や性質が互いによく似ていること。「相似した構造の建物」2 一つの図形を拡大または縮小した関係にあること。3 異種の生物の器官で、発生的には異なるが、機能が同じであるために形態が似ている現象。



合同とは 相似とは
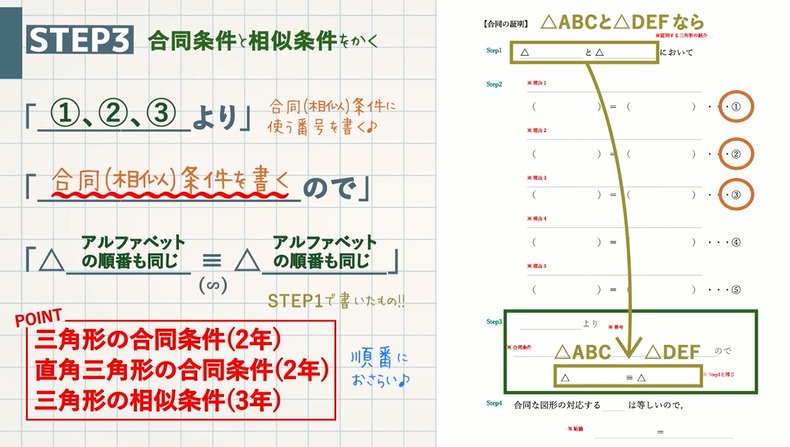



証明 合同 相似 が苦手な人へ 教遊者
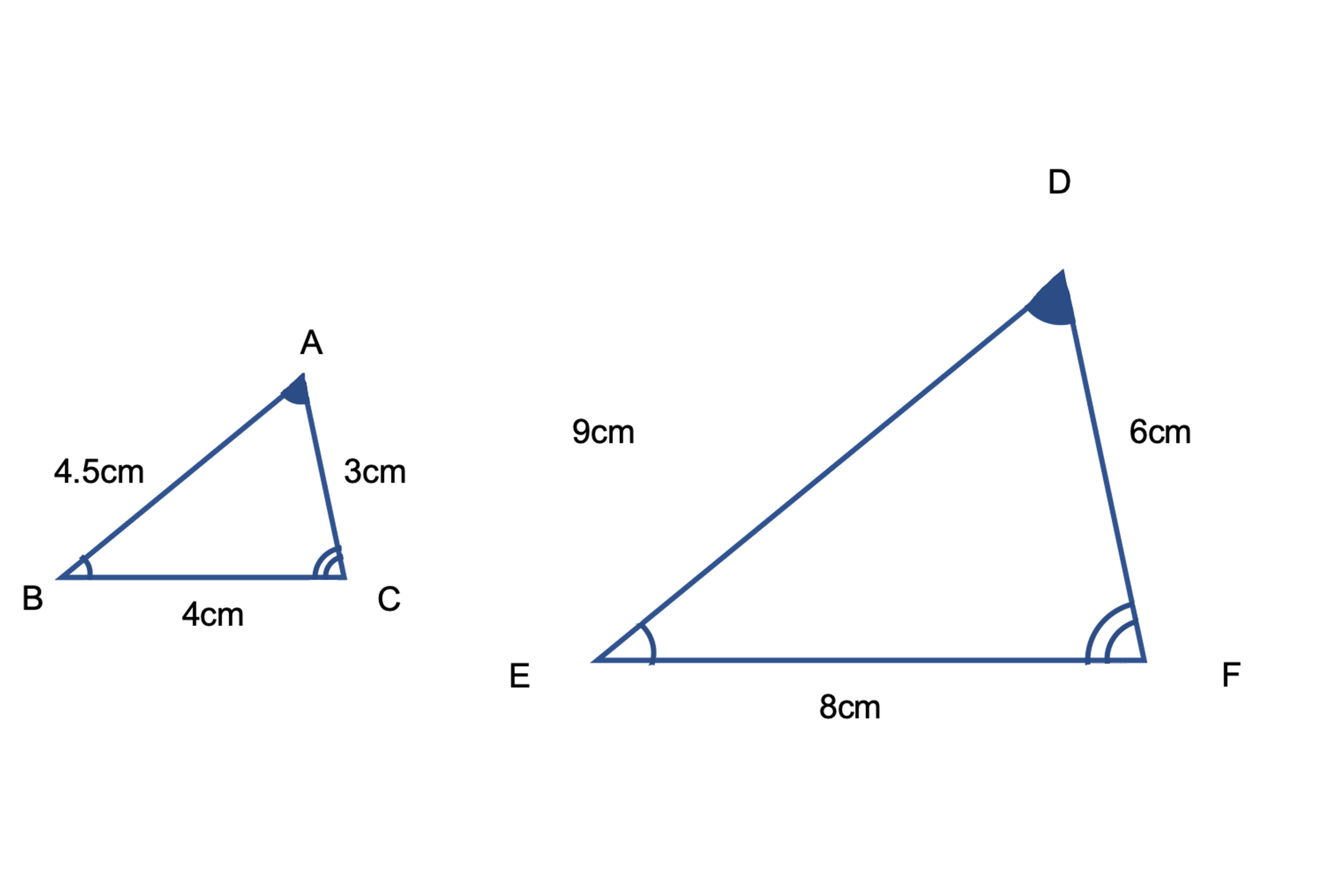
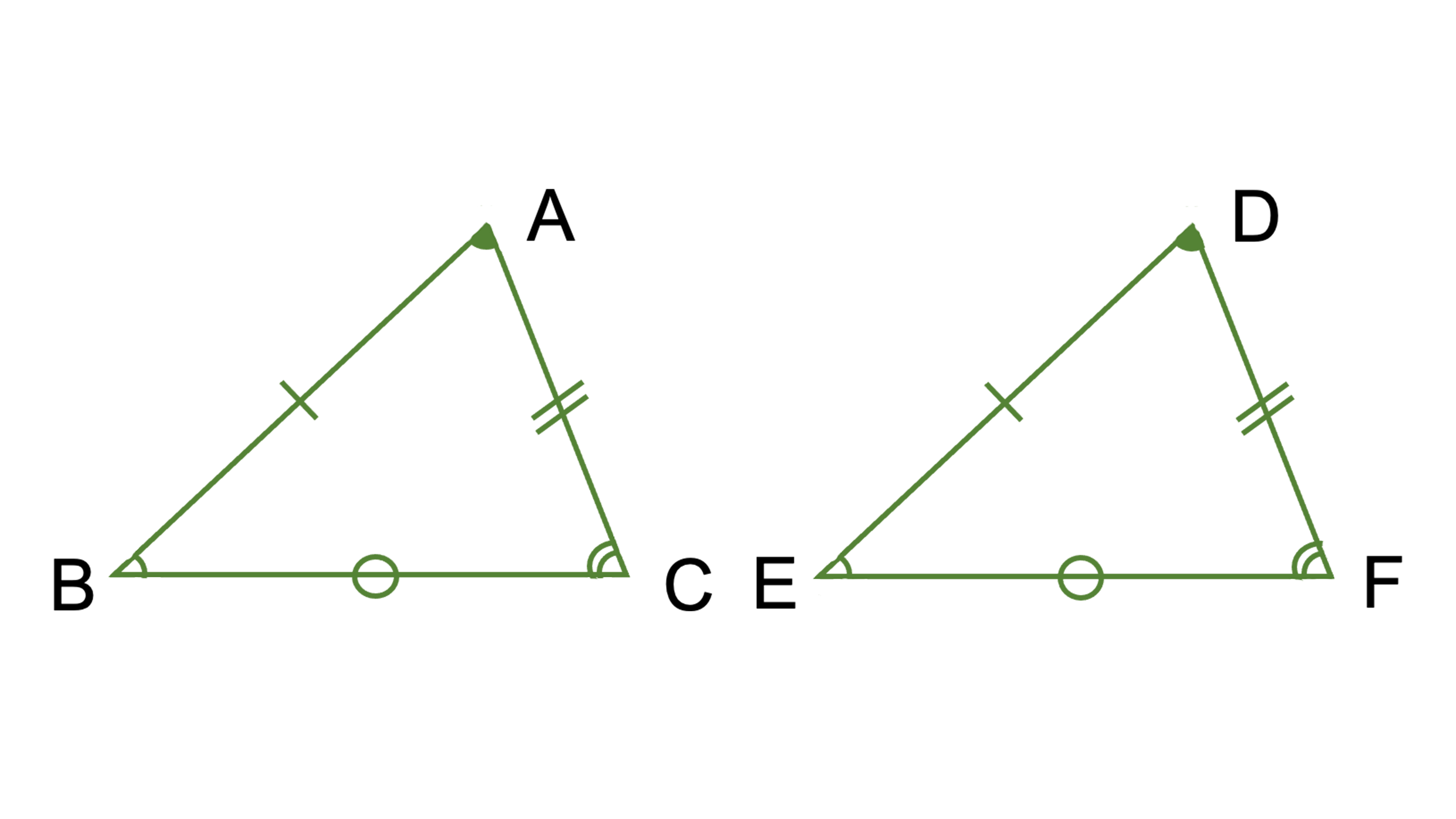
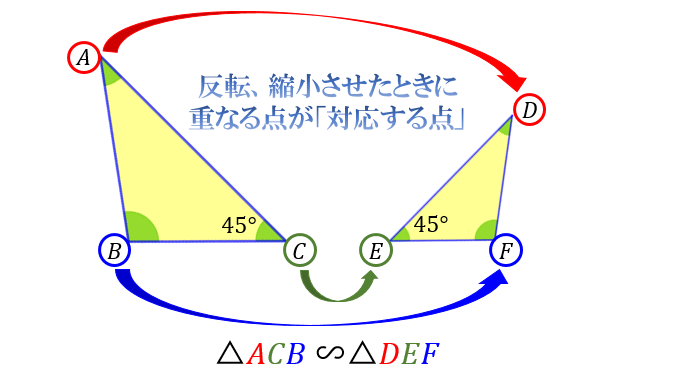
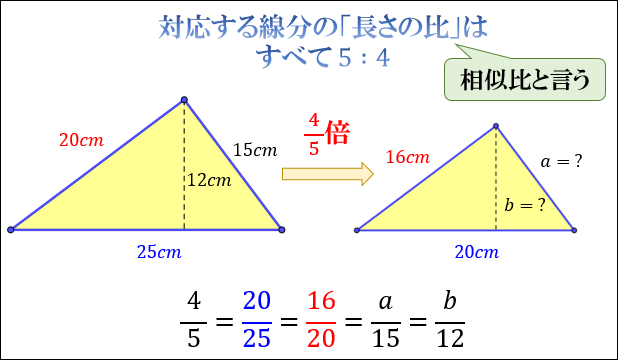
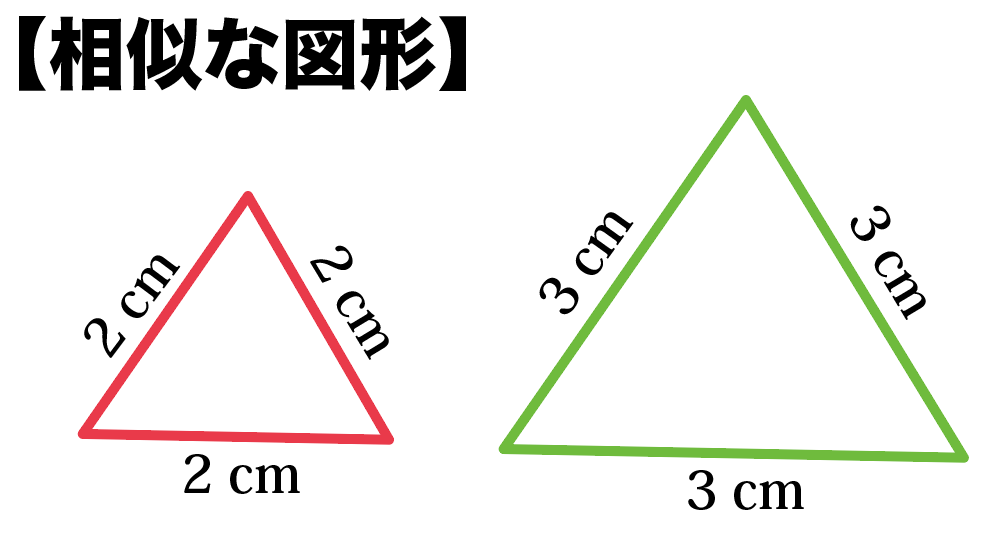
11/7/18 その意味・合同との違い・相似な図形が持つ性質について Tooda Yuuto 18年7月11日 / 18年7月13日 「同じ形のまま拡大・縮小した図形である」ことを、 相似 と言います。 たとえば、下図の三角形 D E F は「三角形 A B C の形を変えることなく 1 2 倍に縮小した図形」です。 このように、大きさは違っても形がまったく同じ図形であるとき 「三角形 A B C と三角形相似とは、一言で言うと 「形は同じだけど、大きさが違う」という関係のことです。 つまり、拡大と縮小の関係です。 合同とは!?12/6/19 数学 > 数学 中学生数学苦手No2!?




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
相似変換反転変換について議論する これらの変換はすべて 2 つの実数変数あ るいは 1 つの複素変数のどちらかの分数線形関数によって表される 61 アフィン変換 アフィン変換は, 平面変換のなかでも重要なものである それは運動の自然な一般化 であるA:a´= b:b´= c:c´ (相似条件) (2) のように,合同条件については辺どうしが等しい関係であること,相似条件については 組にしてとった比 どうしが等しい関係であることの違いです。 しかし,生徒の覚えやすさの観点から,できれば合同条件と相似条件の表現を統一してほしいというご意見もたくさんいただいておりました。 今回,新学習指導要領のもと26/4/21 ごう‐どう〔ガフ‐〕合同の解説 名(スル) 独立している二つ以上のものが一つになること。 また、一つに合わせること。 「二社が合同して計画した事業」「日中合同登山隊」 名・形動 数学で、二つの図形が重ね合わせることのできる関係にあること。 図形Aと図形Bが互いに合同であるとき、記号≡を用いてA≡Bと書き表す。 「合同な三角形」



相似条件




3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ
数学用語と記号ものがたり 元 富士短期大学教授 片野善一郎 著 A5判/0頁/定価2750円(本体2500円+税10%)/03年8月発行 ISBN (旧ISBN ) C3041 小学校から高等学校の教科書で目にする数学の「用語と記号」がどのような考えで創ら8/2/ 算数・数学の合同と相似は、 英語でどのようにいうのか? この記事で図と共に紹介していきます。 合同と相似の用語 合同 「序数」と「基数」の英語 違いをマスターしよう!6/3/21 合同式(mod)を使うメリット 表記簡略化による本質的な嬉しさ 「 12 12 12 と 7 7 7 を 5 5 5 で割った余りは等しい」と書くよりも 「 12 ≡ 7 (m o d 5) 12\equiv 7\pmod{5} 12 ≡ 7 (mod 5) 」と書く方が楽です。 ほとんど差がないように感じますが,記述式で複雑な問題になると上記のような文言を大量に書く必要
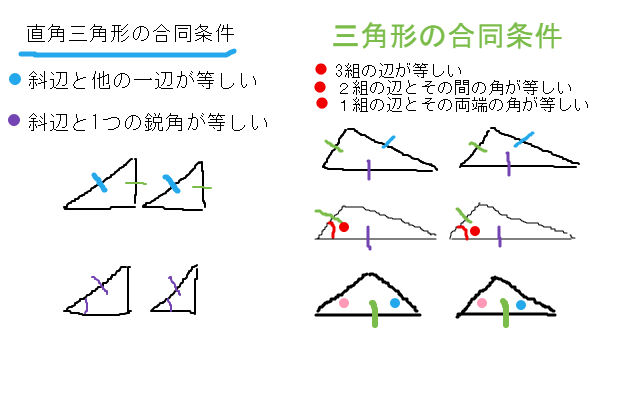



三角形 合同 相似条件 直角三角形の合同条件 中学数学 理科 寺子屋塾の復習サイト
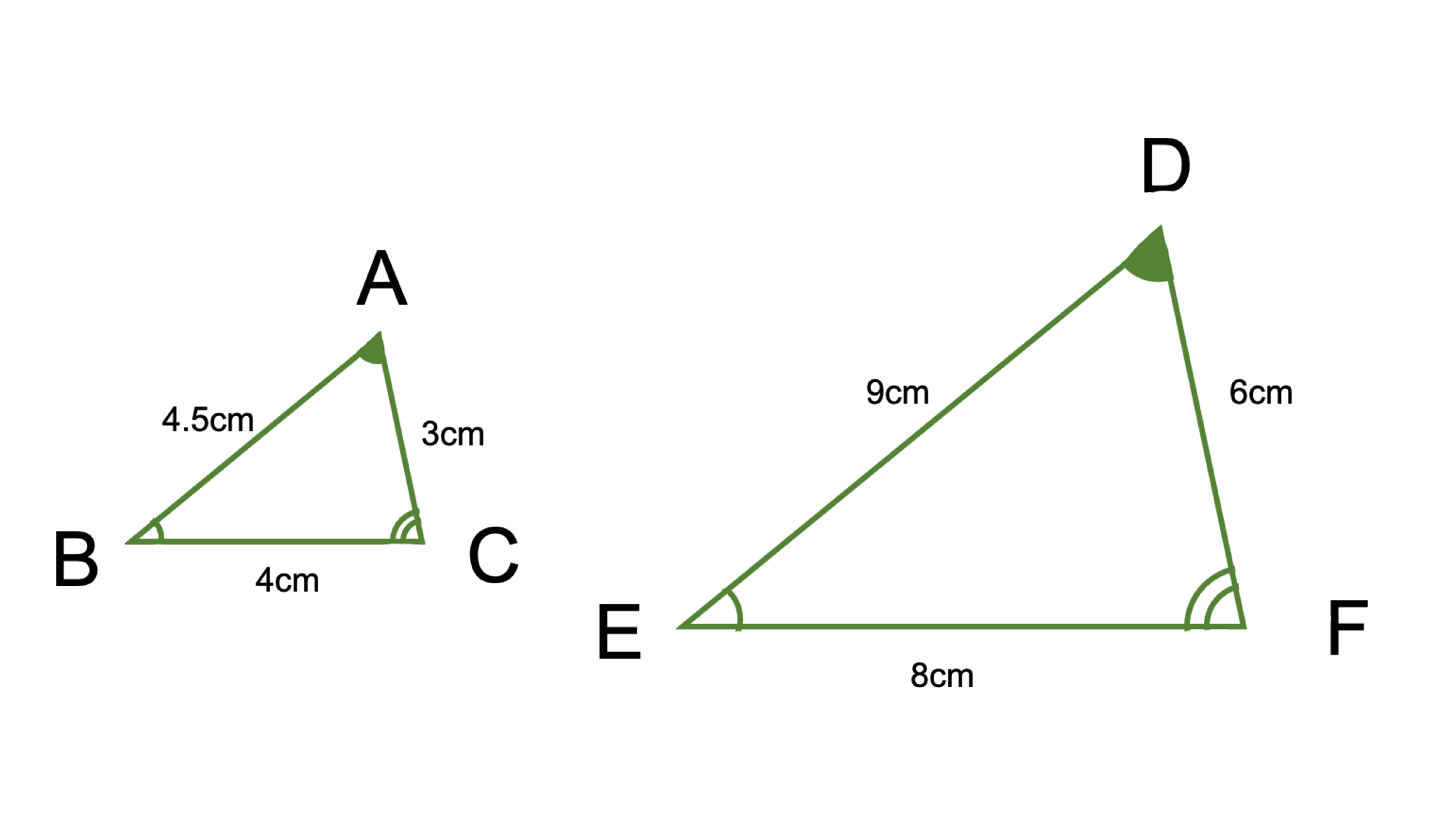



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
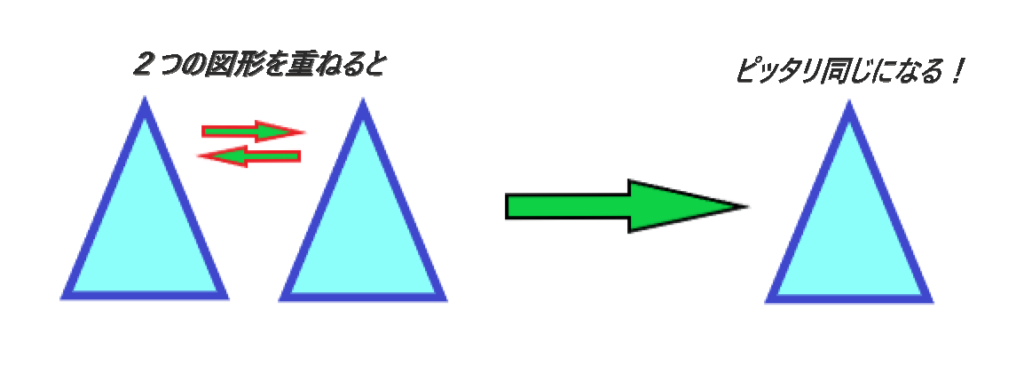
・合同、相似の概念 ・相似や合同といった図形の測定を用いて区別できるようにする。 ・合同、相似の条件 ・公理などを設けて証明を行うことは考えない。 現在との違い 昭和26 年 ・合、相似図形の拡大・縮小 図形の位置や形や大きさを変えることを図形の変換といい,合同変換,相似変換,アフィン変換,射影変換,位相変換などがありますが,小学校では, 合同変換 (移動)形,大きさを変えないで,位置だけを変える変換 相似変換 (拡大,縮小)大きさは変えるが,形は変えない変換 の2つを扱うことになっています。 また,小学校では「相似合同とは、 2つの図形の形と大きさが完全に一致すること を表しています。 分かりやすく説明すると、2つの図形を重ね合わせて形も大きさもピッタリ同じになることです。 説明だけを見るとかなり簡単に思えますが、実際に問題を解く際は教科書やプリントに描いてある図形を動かすことはできませんよね。 それでは一体どうすれば合同であることを証明できるの




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



証明 合同 相似 が苦手な人へ 教遊者
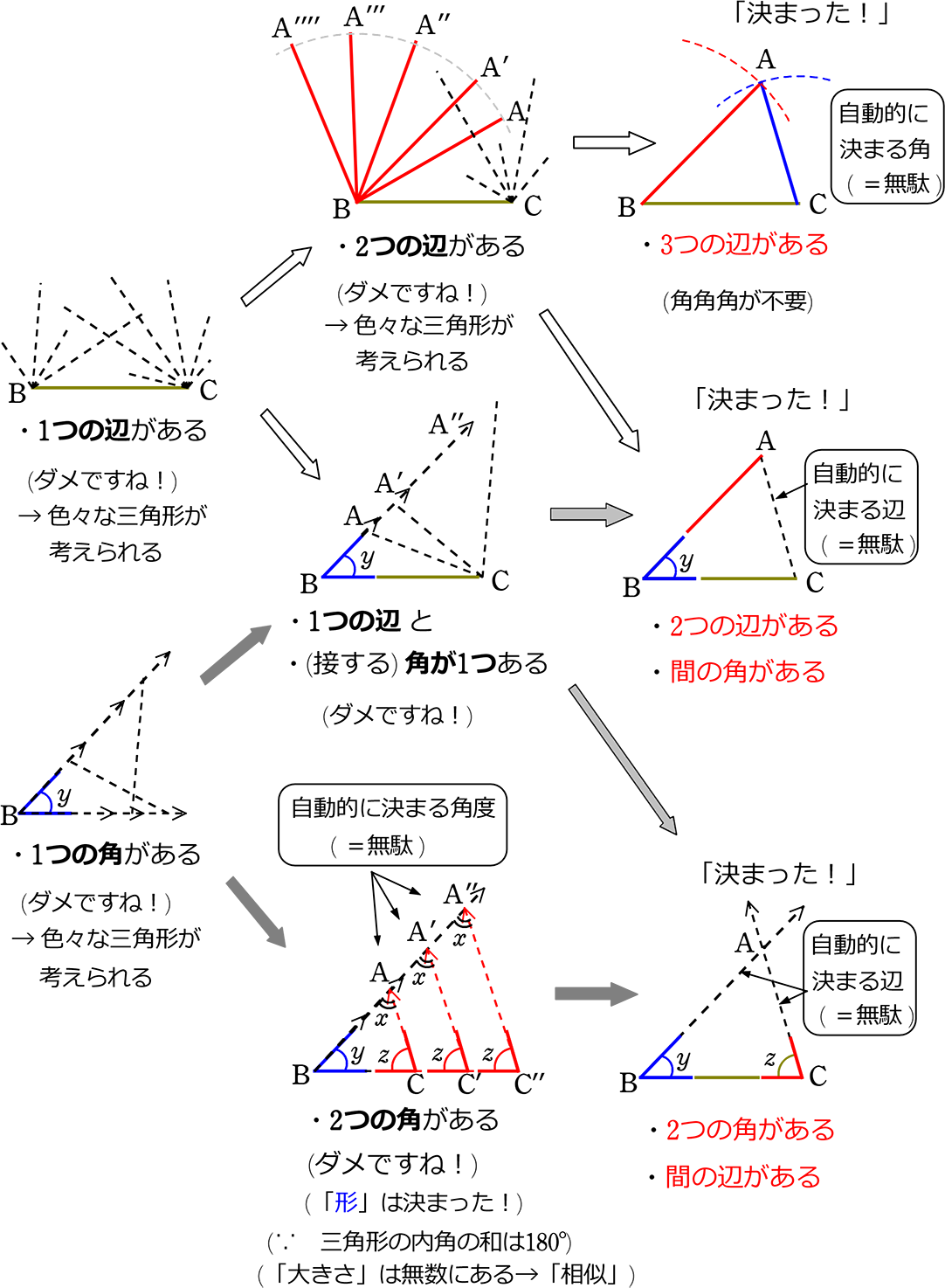
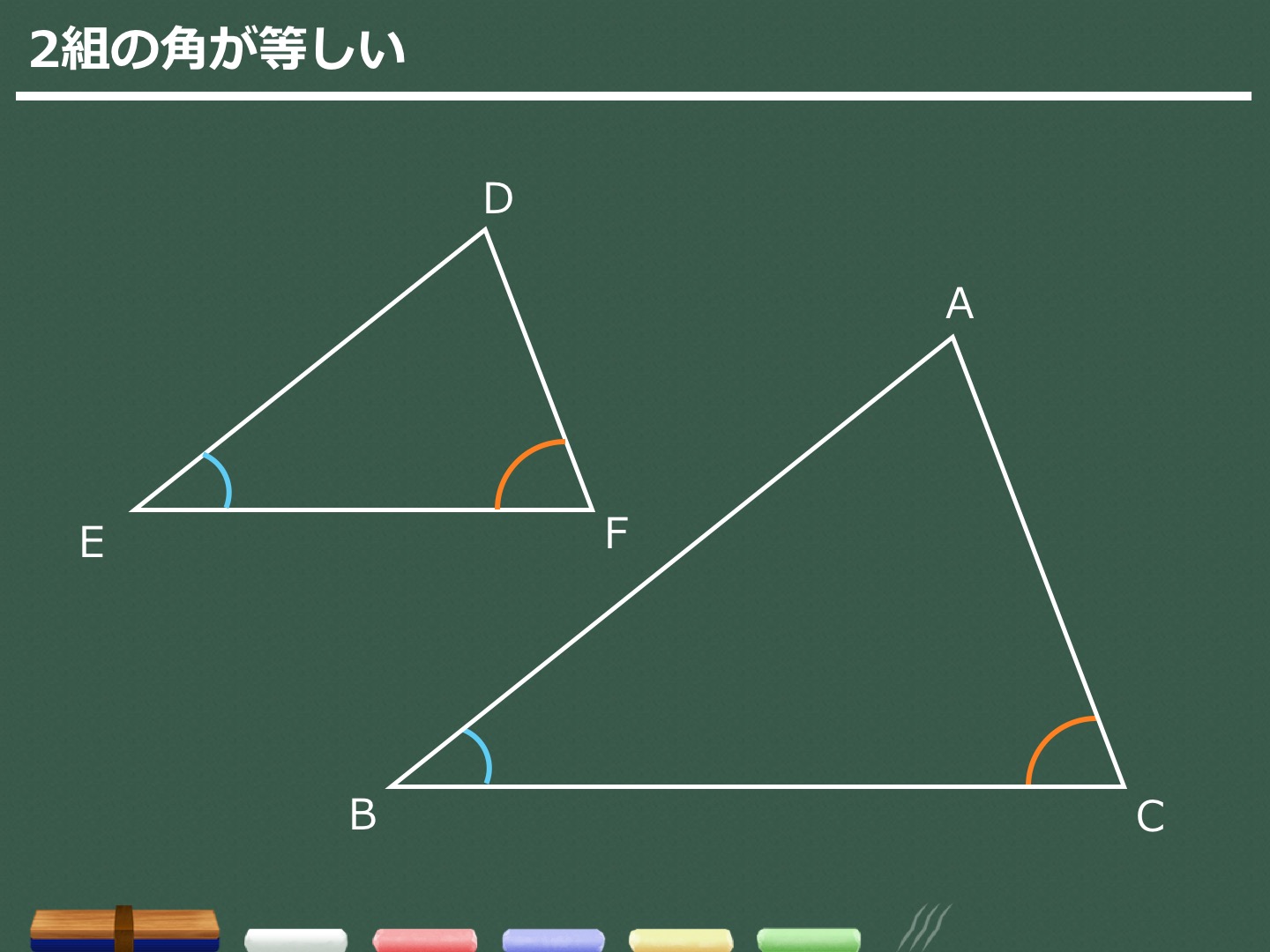
24/7/18 相似条件と合同条件の違いとは? Tooda Yuuto 18年7月24日 2つの三角形が合同であることを示すための条件を、 三角形の合同条件 と言います。 以下の3つの合同条件のうち、 どれか1つでも成り立っている なら「それらの三角形は合同である」ということができます。 条件① 3組の辺がそれぞれ等しい 条件② 2組の辺とその間の角がそれぞれ等しい 条件③ 1証明問題をわかりやすく解説!相似条件との違い スポンサーリンク 三角形の相似条件はなぜ3つ? 相似と合同の違いについて理解できたところで、いよいよ三角形の相似条件 2つの角がそれぞれ等しい 超重要 3組の辺の比がそれぞれ等しい<相似の定義> 1つの図形を,形を変えずに一定の割合に拡大,または縮小して得られる図形は,もと の図形と相似である。 <相似な図形の性質> 相似な図形では,対応する部分の長さの比はすべて等しく,対応する角の大きさはそれ ぞれ等しい。




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ
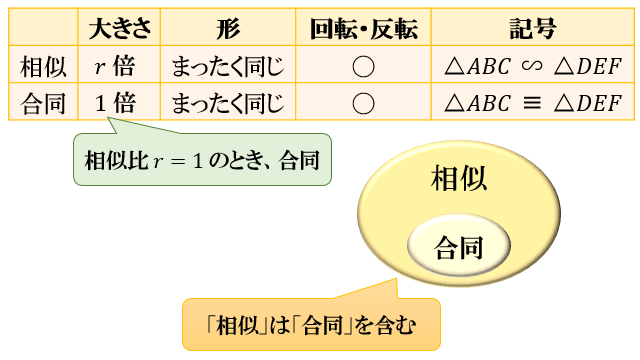
それでは合同と相似をまとめます。 まとめ 合同は 形も大きさも同じ。 対応する角の大きさ、対応する辺の長さは等しい。 まとめ 相似は 形は同じ。大きさは違う。 対応する角の大きさは等しい;合同の復習(じゅんび)(p71) 「右の三角形と合同な三角形をノートに描きましょう。」 「3 通りの描き方があるよ。」 流れ 合同、相似な図形をみつける→方眼用紙を使った作図→合同条件を使った作図→一点を中 心にした作図→縮図の利用




折り返し長方形と相似の証明 中3数学 Youtube




合同とは 相似とは




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




証明 合同 相似 が苦手な人へ 教遊者



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam




中3 数学 相似2 相似比 9分 Youtube




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく



1



神奈川県相模原市緑区の個別指導塾 ナビ個別指導学院相模原橋本校ホームページ 相似と合同の違い




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




合同とは 相似とは



相似と合同の違いは Yahoo 知恵袋



証明 合同 相似 が苦手な人へ 教遊者



三角形の相似 理数系無料オンライン学習 Kori



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support
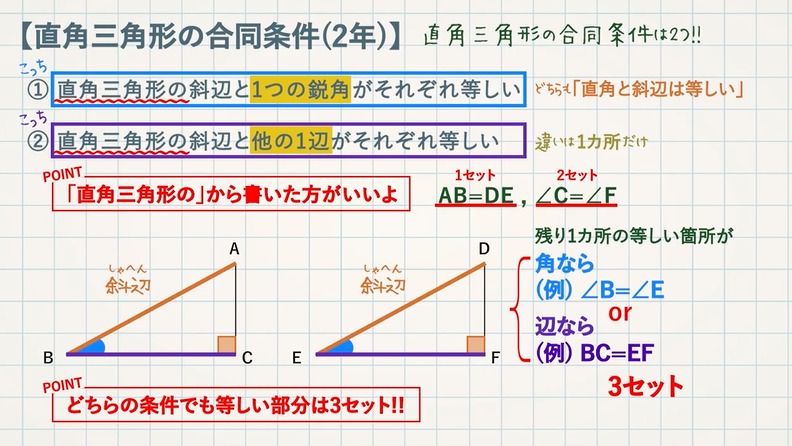



証明 合同 相似 が苦手な人へ 教遊者




三角形の相似条件




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学



相似と合同の違い 見分け方もわかりません Yahoo 知恵袋
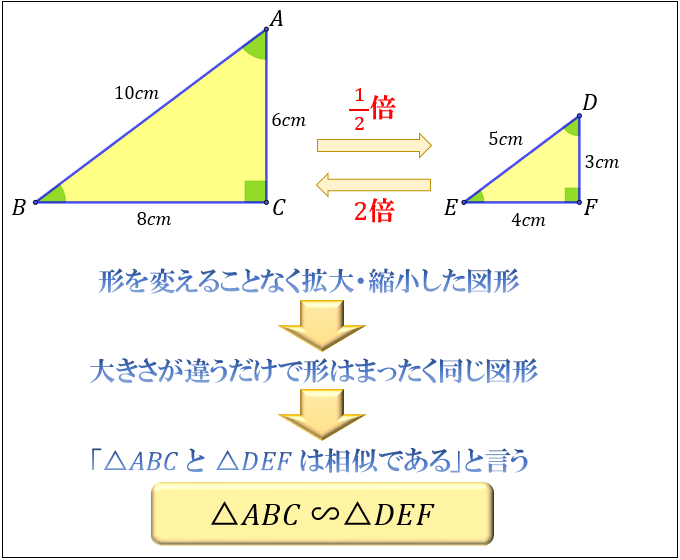



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



相似とは 三角形の相似条件 記号 相似比 面積比 証明問題 受験辞典
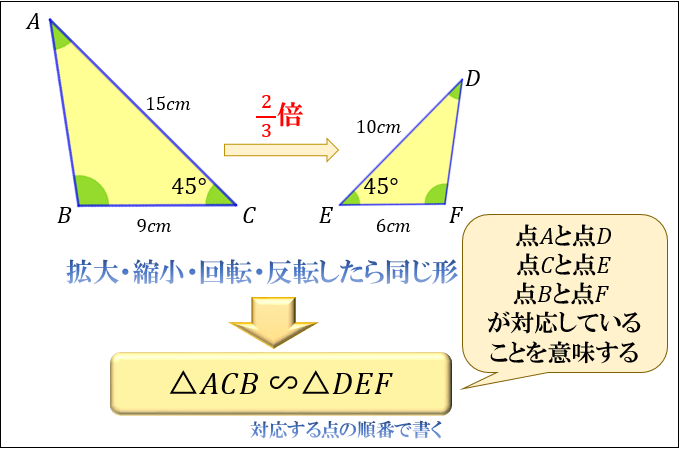



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ
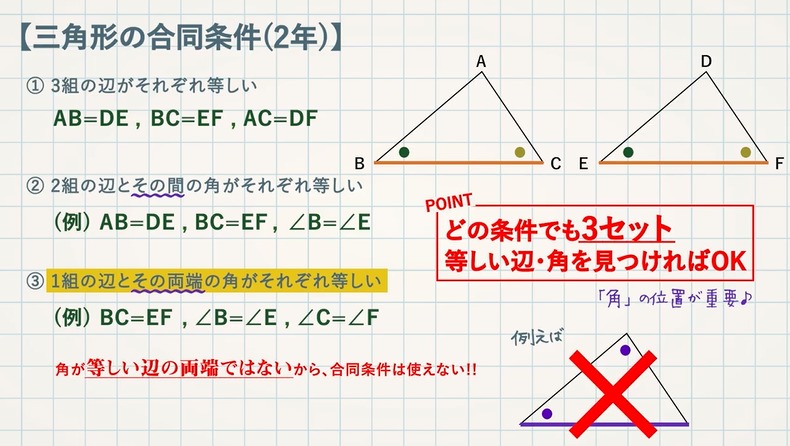



証明 合同 相似 が苦手な人へ 教遊者




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



相似と合同の違いは Yahoo 知恵袋




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




保存版 三角形の合同条件と相似条件の6つのまとめ Qikeru 学びを楽しくわかりやすく



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




相似条件とは 三角形の相似条件はなぜ3つなの 証明問題アリ 遊ぶ数学




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



3



中学の図形証明問題 合同 相似 の解き方と証明の書き方ポイント



合同 相似の英語をマスターしよう 英語独学マスター




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



証明 合同 相似 が苦手な人へ 教遊者



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



中学数学 図形の合同 図形の性質



3



合同 相似の英語をマスターしよう 英語独学マスター



Airx8l Pcmnnnm




図形の合同 Wikipedia




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



相似とは何か その意味 合同との違い 相似な図形が持つ性質について アタリマエ



三角形の合同条件 相似条件と合同条件の違いとは アタリマエ




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



証明 合同 相似 が苦手な人へ 教遊者



3分でわかる 三角形の相似の性質と条件 証明問題の解き方 合格サプリ



1




記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく



相似の条件と合同の条件何が違いますか なるはやで教えてください お願いし Yahoo 知恵袋
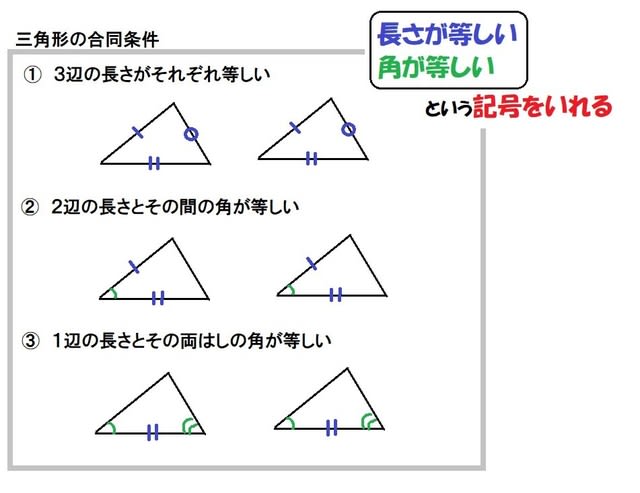



合同な図形 小5 合同条件は超重要 算数の教え方教えますmother S Math Happy Study Support




相似条件



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス
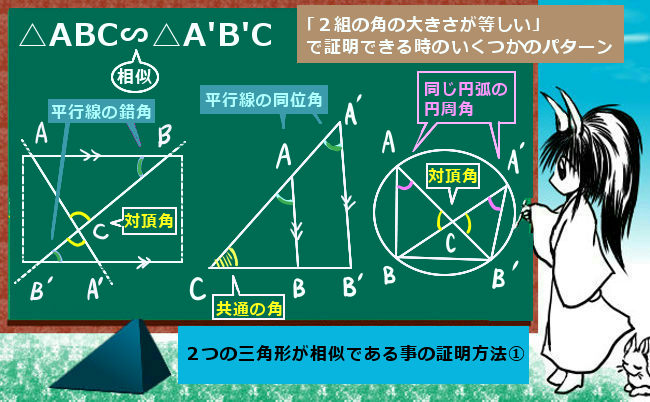



三角形の相似 理数系無料オンライン学習 Kori



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典




記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス
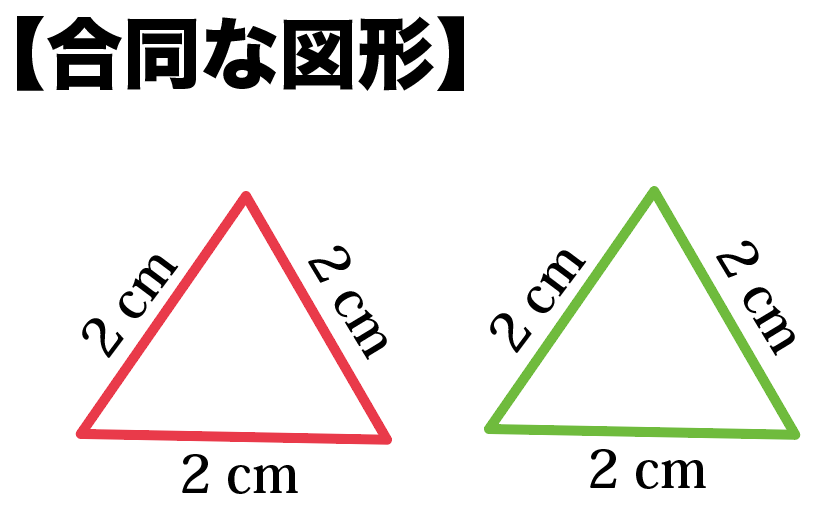



知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学



相似と合同は同じことですか 中2の授業で三角形の合同をならったの Yahoo 知恵袋




合同 相似の英語をマスターしよう 英語独学マスター




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学
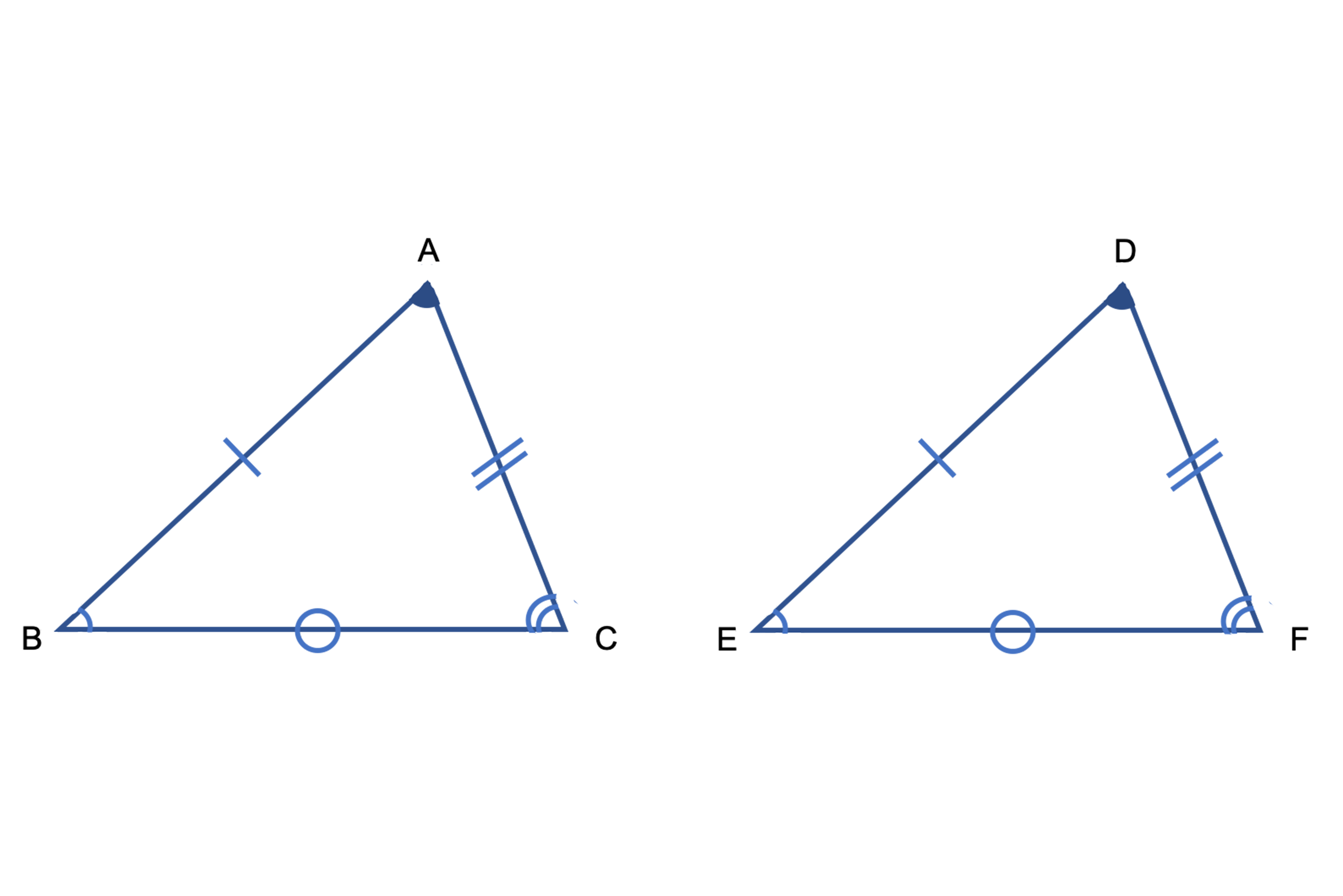



記号にすると と 三角形の 合同 と 相似 の違いをまとめよう 受験に関する豆知識 学習塾ランキング検索総合サイト 塾プラス




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



合同 相似の英語をマスターしよう 英語独学マスター



知っておきたい 相似と合同の3つの違い Qikeru 学びを楽しくわかりやすく




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題



相似 三角形の相似条件 記号や証明問題も Studyplus スタディプラス




証明 合同 相似 が苦手な人へ 教遊者



合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam



合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam




中学生 数学苦手no 2 証明問題 合同 相似 の解き方 学習内容解説ブログ
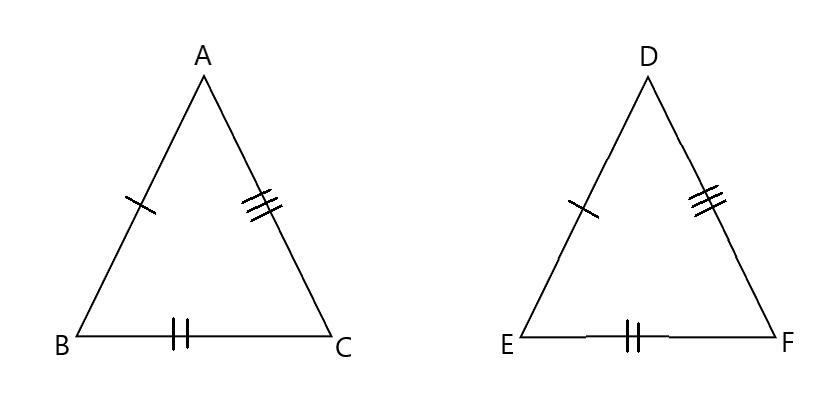



合同と相似とは 演習問題にチャレンジ 個別指導のオンライン家庭教師wam




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



三角形の相似 理数系無料オンライン学習 Kori




三角形の合同条件 相似条件と合同条件の違いとは アタリマエ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



0 件のコメント:
コメントを投稿